La paradoja de Simpson, también llamada efecto de Yule-Simpson es una paradoja o antilogía y sugiere una idea lógicamente contradictoria u opuesta a lo que se considera verdadero a la opinión. La paradoja de Simpson destaca un concepto importante sobre los datos: la necesidad de una buena intuición con respecto al mundo real y cómo la mayoría de los datos son una representación de dimensión finita de un dominio mucho más grande y complejo.
¿Qué es la paradoja de Simpson?
La paradoja de Simpson, consiste en la desaparición o inversión de una relación entre diferentes variables cuando los datos se agrupan de forma diferente, en función de otra variable no considerada previamente. Aunque otros autores habían mencionado el efecto anteriormente, fue Simpson el primero que publicó un trabajo de carácter técnico en el que la describía.
La paradoja de Simpson es más fácil de entender mediante una visualización de datos como la siguiente. La idea básica es que una correlación elevada encontrada entre dos variables puede ser interpretada erróneamente, si una tercera variable usada para separar en grupos los datos analizados conlleva implícita otra asociación que puede ser también relevante, pero de signo contrario. Por lo tanto, el orden de selección de variables cuando se analizan correlaciones es importante y, como siempre, una inspección visual previa de los datos puede ser de ayuda.
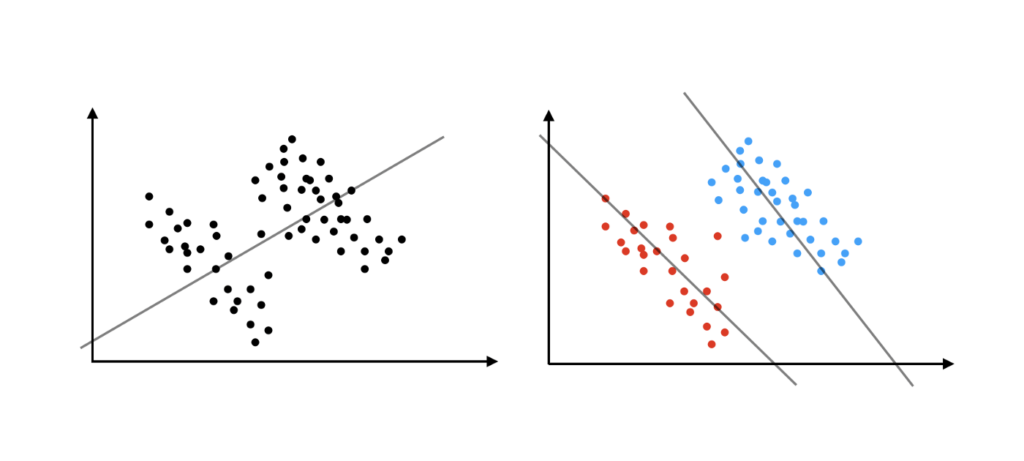
¿Por qué ocurre la paradoja de Simpson?
La paradoja de Simpson ocurre porque la desagregación de los datos (por ejemplo, dividirlos en subgrupos) puede causar que ciertos subgrupos tengan una representación desequilibrada en comparación con otros subgrupos. Esto puede deberse a la relación entre las variables, o simplemente a la forma en que los datos se dividieron en subgrupos.
El famoso ejemplo de UC Berkeley
Un ejemplo famoso de la paradoja de Simpson aparece en los datos de admisión para la escuela de posgrado en UC Berkeley en 1973. Al observar los datos de admisión de posgrado en general, parecía que los hombres tenían más probabilidades de ser admitidos que las mujeres, pero al observar los datos de cada departamento individualmente, los hombres tenían menos probabilidades de ser admitidos que las mujeres. Y sucede porque:
- Los diferentes departamentos tenían índices de aceptación muy diferentes (algunos eran mucho más «difíciles» de ingresar que otros).
- Más mujeres aplicaron a los departamentos «más duros».
- Por lo tanto, las mujeres tuvieron una tasa de aceptación más baja en conjunto.
Esto nos lleva a preguntarnos: ¿cuál es la visión correcta? ¿Los hombres o las mujeres tienen una mayor tasa de aceptación? ¿Existe un sesgo de género en las admisiones en esta universidad?
En este caso, parece más razonable concluir que mirar las tasas de admisión por departamento tiene más sentido y que la vista desagregada es correcta.
Los juegos de beisbol
Los promedios de bateo de dos jugadores de béisbol famosos, Derek Jeter y David Justice, de 1995 y 1996. David Justice tuvo un promedio de bateo más alto tanto en 1995 como en 1996 individualmente, pero Derek Jeter tuvo un promedio de bateo más alto en los dos años combinados. Y explicamos que pasó:
- Ambos jugadores tuvieron promedios de bateo significativamente más altos en 1996 que en 1995.
- Derek Jeter tuvo muchos más turnos al bate en 1996; David Justice tenía significativamente más en 1995.
- Por lo tanto, Derek Jeter tuvo un promedio de bateo más alto en el agregado.
Una vez más, podemos preguntarnos: ¿cuál es la vista correcta? ¿Fue Derek Jeter o David Justice mejor bateador? En este caso, parece más razonable concluir que el punto de vista agregado es el punto de vista correcto y que Derek Jeter fue el mejor bateador durante los dos años.
Es difícil sacar conclusiones de los datos cuando los datos nos cuentan dos historias opuestas al mismo tiempo. Uno podría estar tentado a pensar que la vista desagregada siempre es mejor ya que contiene más información, pero es posible que desagregar una variable adicional proporcione una perspectiva innecesaria o confusa.
Datos de casos graves de COVID-19
Para los casos de eficiencia vs severidad de la vacunación por COVD 19 en Israel
De los 515 pacientes actualmente hospitalizados con cuadros graves en el país, 301 (58%) de estos casos era gente completamente vacunada, es decir, habían recibido dos dosis de Pfizer. El 60% de todos los hospitalizados graves por covid-19 era gente vacunada. ¿Significa eso que la vacuna tiene una baja eficacia? ¿Que es estadísticamente mejor no vacunarse que hacerlo para evitar los cuadros graves?
No precisamente. Significa que faltan datos para entender el contexto. Si en ese entonces había en torno a un 80% de personas mayores de 12 años vacunadas, hay mucha, mucha más gente en ese grupo que en el de no vacunados, así que la comparativa no es proporcional. Por eso lo primero que habría que hacer es estimar las tasas de hospitalización con cuadros graves segregando vacunados de no vacunados.


Pingback: 8 formas en que un científico de datos usa la estadística -Yizinet