La ganancia de información y entropía están involucradas en muchos temas de aprendizaje automático, como el árbol de decisión y el bosque aleatorio. Necesitamos aprender el papel de la ganancia de información y la entropía en la construcción de un modelo de machine learning. Nos centraremos en la parte estadística de la ganancia de información y entropía.
¿Qué es entropía?
La teoría de la información es una parte de las matemáticas relacionado con la transmisión de datos a través de un canal ruidoso. Una piedra angular de la teoría de la información es la idea de cuantificar cuánta información hay en un mensaje. De manera más general, esto se puede usar para cuantificar la información en un evento y una variable aleatoria, llamada entropía.
Calcular información y entropía es una herramienta útil en machine learning y se utiliza como base para técnicas como la selección de características, la construcción de árboles de decisión y, de manera más general, el ajuste de modelos de clasificación. Como tal, un científico de datos requiere una gran comprensión e intuición de la información y la entropía.
La entropía es una medida de cualquier tipo de incertidumbre que está presente en los datos. Se puede medir utilizando la fórmula:
Donde
¿Qué es ganancia de información?
La ganancia de información indica cuánta información nos brinda una característica particular o una variable particular sobre los resultados finales. Se puede medir utilizando la fórmula
Donde
Ejemplo práctico
Ejemplifiquemos la situación donde hay que pronosticar si el partido se puede jugar o no, indicando las condiciones meteorológicas. Las variables predictoras aquí son el pronóstico, la humedad y el viento.
El valor de la variable objetivo es que se pueda o no jugar el juego. La predicción «No» significa que las condiciones climáticas no son buenas y por lo tanto, no se puede jugar. La predicción «Sí» significa que se puede jugar, por lo que la jugada tiene un valor que es «sí» o «no». Ahora, para resolver tal problema, hacemos uso de un árbol de decisión.
Consideremos un árbol donde cada rama del árbol denota alguna decisión. Cada rama se conoce como un nodo de rama, y en cada rama, debemos decidir de tal manera que pueda obtener un resultado al final de la rama. En la siguiente imagen muestra que de las 14 observaciones, 9 observaciones dan como resultado un sí, lo que significa que de los 14 días, el partido se puede jugar solo en 9 días. Así que aquí si ven los días 1, 2, 8, 9 y 11, el panorama ha sido soleado. Básicamente, estamos tratando de agrupar conjuntos de datos según la perspectiva. Cuando hace sol, tenemos dos “Sí” y tres “No”; cuando la perspectiva está nublada, tenemos los cuatro como Sí, lo que significa que en los 4 días en que la perspectiva estaba nublada, podemos jugar el juego.
Cuando se trata de lluvia, tenemos tres «Sí» y dos «No». La decisión se puede tomar según la variable de perspectiva en el nodo raíz. Entonces, el nodo raíz es el nodo superior en un árbol de decisión. Ahora, lo que hemos hecho aquí es que hemos creado un árbol de decisiones que comienza con el nodo pronóstico y luego lo dividimos aún más según otros parámetros, como soleado, nublado y lluvioso.
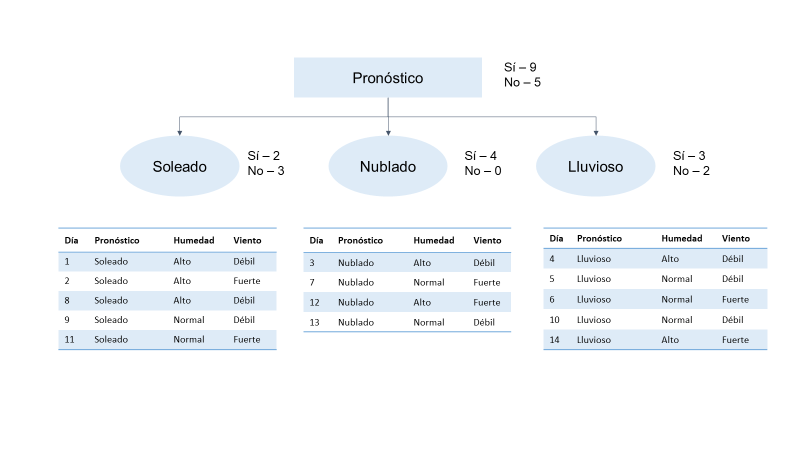
Lo que estamos haciendo es tomar el árbol de decisiones eligiendo la variable de perspectiva en el nodo raíz. El nodo raíz es el nodo superior en un árbol de decisión. El nodo Pronóstico tiene tres ramas que salen: soleado, nublado y lluvioso. Estos tres valores se asignan al nodo de la rama intermedia y se calculan para la posibilidad de jugar igual a «sí». Para ramas soleadas y lluviosas, si es una mezcla de sí y no, dará una salida impura (entrópicamente hablando). Pero cuando se trata de la variable nublada, da como resultado un salida 100% pura (entrópicamente hablando). Esto muestra que la variable nublada dará como resultado una salida definida y cierta. Esto es exactamente lo que se usa para medir la entropía que calcula la impureza o la incertidumbre. Entonces, cuanto menor es la incertidumbre o la entropía de una variable, más significativa es esa variable.
Cuando se trata de días nublados que no tienen impurezas en un conjunto de datos, es un subconjunto puro perfecto. No siempre tenemos suerte y no siempre encontramos variables que den como resultado un subconjunto para medir la entropía. Por lo tanto, cuanto menor sea la entropía de una variable particular, más significativa será esa variable. En el árbol de decisión, el atributo asignado del nodo raíz se considera para el resultado preciso. Esto significa que el nodo raíz debe tener la variable más significativa, razón por la cual elegimos el pronóstico.
El nodo nublado no es una variable sino el subconjunto del nodo raíz pronóstico. Ahora la pregunta es ¿Cómo decidir qué variable o atributo divide mejor los datos?. Cuando se trata de árboles de decisión, ganancia de información y entropía, nos ayudará a comprender qué variable dividirá mejor el conjunto de datos o qué variable se usa para asignar al nodo raíz. Las variables asignadas al nodo raíz se dividirán según el conjunto de datos con las variables más significativas.
Cálculo de la ganancia de la información
De acuerdo a la fórmulas anteriores, podemos encontrar la ganancia de información y la entropía. Del total de 14 instancias que vimos, 9 dijeron que sí y 5 dijeron que no, lo que significa que no puedes jugar ese día en particular. Entonces podemos calcular la entropía usando el árbol de decisión anterior para la predicción. Susutituimos los valores en la fórmula:
Cuando sustituye los valores en la fórmula, obtiene un valor de 0.94. Esta es la entropía y esta es la incertidumbre de los datos presentes en la muestra. Ahora, para asegurarnos de elegir la mejor variable para el nodo raíz, veamos las posibles combinaciones que puede usar en el nodo raíz.
Todas las combinaciones posibles que puede usar en el nodo raíz se muestran en la siguiente figura. La combinación posible puede ser pronóstico, viento, humedad o temperatura. Estas son cuatro variables y puede tener cualquiera de estas variables como su nodo raíz. Pero ¿Cómo selecciona la variable que mejor se ajusta al nodo raíz? Aquí, podemos usar la ganancia de información y la entropía. Por lo tanto, la tarea es encontrar la ganancia de información para cada uno de estos atributos, es decir, para perspectiva, viento, humedad y temperatura. Debe elegirse la variable que resulte en la mayor ganancia de información porque proporciona la información de salida más precisa.
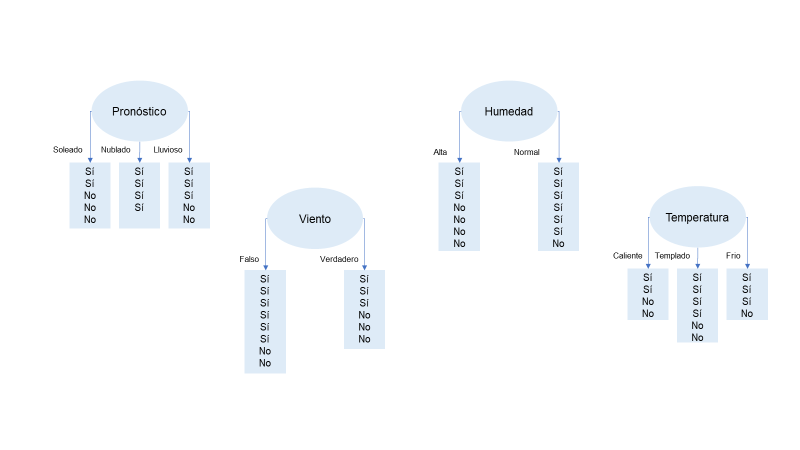
La ganancia de información para el atributo viento calculará primero ese atributo; aquí, tenemos seis instancias de verdadero y ocho instancias de falso. Cuando sustituyamo todos los valores en la fórmula obtendremos el valor para la ganancia de información:
Análogamente, calculamos la ganancia de información de la perspectiva del atributo soleado. De un total de 14 instancias, tenemos 5 instancias de soleado, 4 instancias de nublado y 5 instancias de lluvia. Para soleado, tenemos tres sí y dos no; para nublado, tenemos los cuatro como Sí; y para lluvioso, tenemos tres sí y dos no. Entonces, cuando calcule la ganancia de información de la variable de pronóstico, obtendremos un valor de 0.247. En comparación con este valor, la ganancia de información del atributo viento es buena, es decir, 0.247 para la ganancia de información.
Similarmente, la ganancia de información del atributo humedad. Aquí encontramos siete instancias que ven «alto» y siete instancias ven «normal». El valor «alto» en el nodo de rama tiene siete instancias y el resto del valor «normal». De manera similar, en la rama normal, tenemos siete instancias que dicen que sí y una instancia que dice que no. Al calcular la ganancia de información para la variable de humedad, obtendremos un valor de 0.151. Este también es un valor muy decente, pero en comparación con la ganancia de información de pronóstico, es menor.
Ahora, observemos la ganancia de información de los atributos como temperatura. La temperatura puede tener tres atributos básicos: caliente, templado y frío. Bajo caliente, tenemos dos instancias sí y dos instancias no; bajo suave, tenemos cuatro instancias sí y dos instancias no; y bajo frío, tenemos tres instancias de sí y una instancia de no. Si calculamos la ganancia de información para este atributo, obtendremos un valor de 0.029.
Para resumir, si observamos la ganancia de información para cada una de estas variables, verá que para pronóstico, tenemos la ganancia máxima. Tenemos 0.247, que es el valor de ganancia de información más alta, y siempre debemos elegir la variable con la ganancia de información más alta para dividir los datos en el nodo raíz, por eso asignamos la variable de pronóstico en el nodo raíz.

